Calibration des paramètres du modèle par la méthode du BLUE

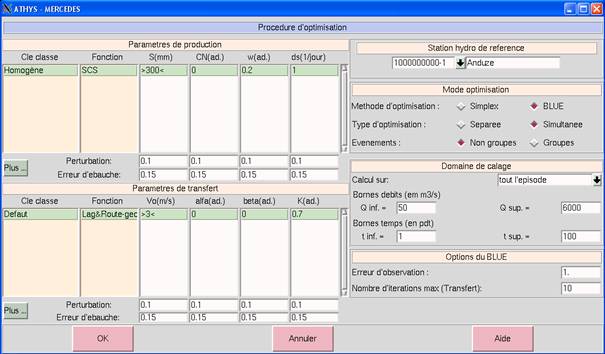- la fonction coût est imposée, et correspond à une pondération de l'écart sur les résultats du modèle et de l'écart sur les paramètres par rapport à leur estimation initiale (cf. Principes du BLUE)

- l'utilisateur doit spécifier les degrés de confiance sur les estimations des paramètres et sur les observations. Les champs correspondant sont accessibles par l'icône Plus, qui opère une bascule avec les champs borne inférieure / borne supérieure.

- l'utilisateur doit également spécifier les pas d'incrémentation (perturbation) pour le calcul de la dérivée de la fonction coût incrémentale. Les champs correspondant sont accessibles par l'icône Plus, qui opère une bascule avec les champs borne inférieure / borne supérieure.

- les nombres d'itérations dans la procédure d'optimisation correspondent à une réalisation effective d'un nombre équivalent d'itérations (contrairement à la méthode du simplex, dans laquelle un critère de proximité de 2 jeux de paramètres successifs permet de sortir de la procédure, avant d'être arrivé au terme du processus itératif)

La touche est une touche à bascule, qui affiche soit les champs des bornes inférieures et supérieures de chaque paramètre, soit le pas d'incrémentation et le degré de confiance associé à chaque paramètre.

Principes du BLUE

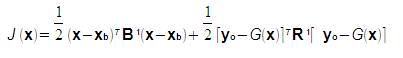
où x est le vecteur de contrôle dont on cherche la valeur optimale, qui minimise la fonction coût, xb l'ébauche = la valeur initiale du vecteur de contrôle,G l'opérateur d'observation généralisé = le modèle, yo le vecteur d'observation = les sorties du modèle, B la matrice des covariances d'erreur d'ébauche et R la matrice des covariances d'erreur d'observation. On note xa l'analyse = la valeur optimale du vecteur de contrôle qui minimise la fonction coût.

Le vecteur de contrôle peut contenir les paramètres d'un modèle, mais aussi les variables d'entrée ou les variables d'état d'un modèle. Le vecteur d'observation contient toutes les variables du système réel que l'on souhaite assimiler : débits, teneurs en eau des sols, vitesses…. L'opérateur d'observation est le modèle qui permet de simuler ces mesures.

Les inverses B⁻¹ et R⁻¹ peuvent être vues comme des matrices de « certitude » qui pondèrent les différentes informations, ébauche ou observations, en fonction du degré de confiance qu'on leur attribue. Enfin, l'analyse est la meilleure estimation du vecteur de contrôle produite par la méthode d'assimilation choisie.

Dans certaines applications, la minimisation de J peut s'avérer fastidieuse et l'on approxime la méthode d'assimilation par sa version incrémentale qui consiste à minimiser :

(2)

où G est l'opérateur d'observation G linéarisé autour de l'ébauche xb et d le vecteur

innovation défini par d=yo−Gxb .

La minimisation de cette fonction quadratique conduit à l'analyse :

xa=xbK[yo-G(xb)] avec K=B⁻¹G^TR⁻¹G⁻¹G^TR⁻¹=BG^TGBG^TR⁻¹ (3)

où K est la matrice de gain qui relie donc l'innovation à l'incrément d'analyse par la relation xa=Kd . Les deux expressions analytiques de K en fonction des matrices B, R et G peuvent être utilisées indifféremment. Cette matrice permet de déterminer la matrice des covariances d'erreur d'analyse A=I−KGB qui peut être utilisée comme une nouvelle matrice de covariances d'erreur d'ébauche lorsque l'analyse xa est utilisée comme nouvelle ébauche pour améliorer l'approximation de J par J inc.

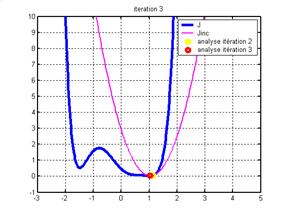
La démarche d'optimisation peut être illustrée par les étapes suivantes :

1. la fonction coût est représentée pour l'ensemble des jeux de paramètres. Le problème est de trouver le jeu optimal des paramètres = celui qui minimise la fonction coût. On va donc chercher à annuler la dérivée de la fonction coût. La dérivée de la fonction coût n'est généralement pas une fonction quadratique dont on peut trouver analytiquement les valeurs nulles. On va donc procéder par itération, en construisant la fonction coût "incrémentale", dont la dérivée est une fonction quadratique.

2. l'ébauche (valeurs initiales des paramètres) ayant été choisie, la fonction coût incrémentale est calculée au voisinage de cette ébauche. La fonction coût incrémentale est une fonction quadratique, dont la dérivée au voisinage de l'ébauche est égale à la dérivée de la fonction coût. Le minimum de la fonction coût incrémental est calculé, et correspond à la valeur de l'analyse. Cette analyse a pour valeur xa=xb+K[yo-G(xb)]

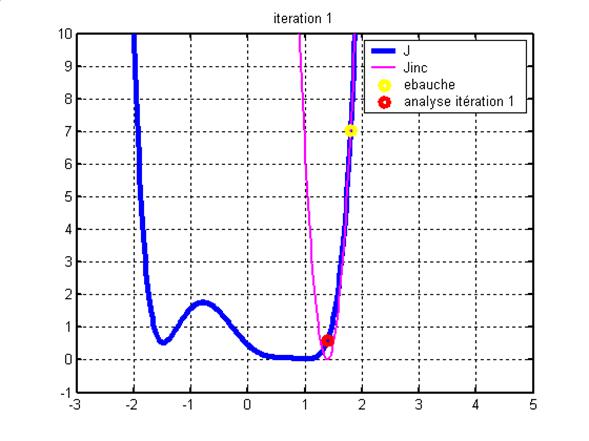
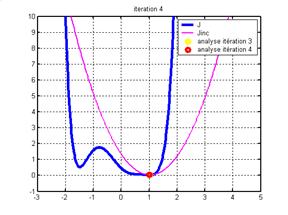
3. la fonction coût incrémentale est de nouveau calculée au voisinage de l'analyse. La minimisation de cette nouvelle fonction incrémentale fournit une nouvelle analyse. L'étape 3 est répétée pour n itérations. Les valeurs correspondant à la minimisation de la fonction coût incrémentale convergent vers le minimum de la fonction coût.

etc…..

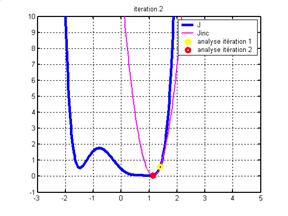Pour plus d'éléments sur cette méthode, le lecteur pourra se référer au lien suivant : http://www.cerfacs.fr/globc/publication/technicalreport/2007/revue_methodes_assimilation/node22.html

Spécificités ATHYS

Le vecteur de contrôle se réduit aux paramètres du modèle. Il n'est pas possible d'optimiser les variables d'entrée ou les variables d'état, sauf si elles apparaissent explicitement comme paramètre du modèle.

Les observations assimilables se réduisent aux débits simulés par les modèles pluie-débit.

La matrice B des covariances d'erreur sur les paramètres du modèle se réduit à la matrice des variances d'erreur sur les variables du vecteur de contrôle les paramètres (on considère que les paramètres sont indépendants), soit :

Par exemple, si un paramètre est déterminé par régression linéaire en fonction d'une variable explicative avec un coefficient de détermination R², la variance d'erreur du paramètre est égale à :

La matrice R des covariances d'erreurs d'observations se réduit à la matrice des variances d'erreurs d'observations (on suppose que les erreurs sur des observations successives ne sont pas corrélées).

Le pas d'itération détermine le voisinage de calcul de l'opérateur dérivé autour de l'analyse fournie à l'issue de chaque itération. Ce pas d'itération est exprimé dans l'unité de celle du paramètre associé.

Cas des paramètres bornés

Le BLUE ne permet pas de faire varier les paramètres entre des bornes explicitement définies. Des bornes peuvent néanmoins être déclarées, et servent à contrôler que les valeurs des paramètres restent comprises dans un intervalle adapté.

Les variations des paramètres sont donc totalement libres, et indépendantes des bornes déclarées. A chaque itération, la nouvelle valeur du paramètre est contrôlée par rapport aux bornes déclarées : si cette valeur se situe à l'extérieur de ces bornes, la procédure est interrompue et le programme stoppé..

Les solutions pour pallier ce problème sont les suivantes :

• modifier les bornes de variation des paramètres
• limiter la variation des paramètres en réduisant l'erreur sur l'ébauche
• limiter la variation des paramètres en réduisant la valeur de la perturbation servant à calculer la fonction coût incrémentale

Partenariat

L'implémentation du BLUE dans ATHYS a été rendue possible par la collaboration avec le CERFACS et le soutien du SCHAPI. Ce travail a été principalement réalisé par Ersin Kilicoglu, sous la direction de Christophe Bouvier et avec la participation d'Anne Crespy et Agnès Crès à HSM, de Sophie Ricci et Olivier Thual au CERFACS, d'Arthur Marchandise au SCHAPI.